Poligoane regulate

în această lecție o să vorbim despre

poligoane regulate și o să găsim

o formulă de calcul pentru latura

apotema și aria unui poligon regulat

în funcție de raza cercului circumscris

acestuia începem cu o definiție

o linie frântă închisă se numește

poligon există două tipuri de poligoane

convexe și concave Poligonul convex

are proprietatea că oricum aș unii

două puncte ale acestuia segmentul

astfel obținut este conținut în

întregime în interiorul Poligonului

în schimb Poligonul concav nu are

această proprietate dacă unelte

exemplu aceste două puncte observăm

că Segmentul determinat este situat

în afara Poligonului În astfel

de poligon se numește poligon Hanca

în continuare o să discutăm dat

despre poligoanele convex urmează

o altă definiție un poligon convex

este regulat dacă are toate laturile

și toate unghiurile congruente

avem aici câteva exemple de poligoane

regulate triunghiul echilateral

pătratul pentagonul Acesta este

un poligon cu cinci laturi hexagonul

este un poligon cu șase laturi

iar decagonul este un poligon cu

10 laturi în continuare să vedem

câteva proprietăți ale poligoanelor

regulate orice poligon regulat

se poate înscrie între un cerc

iar centrul cercului circumscris

unui poligon regulat se mai numește

centrul Poligonului distanța de

la centrul Poligonului la o latură

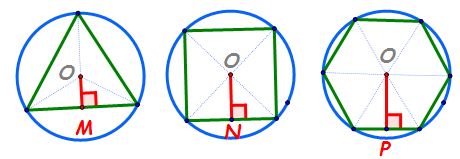
se numește apotemă în prima figură

avem un triunghi echilateral abc

o este centrul triunghiului perpendiculara

din A pe latura b c se numește

apotema având în vedere că un triunghi

are trei laturi putem să ducem

trei apoteme de reținut faptul

că punctul m este situat la mijlocul

laturii BC pentru că triunghiul

b o c este isoscel segmentele desenate

punctat sunt raze b o a o și c

o și ele sunt congruente Așadar

triunghiul boc va fi un triunghi

isoscel iar înălțimea în triunghi

isoscel este și mediană din acest

motiv punctul M va fi situat la

mijlocul laturii triunghiului în

a doua figură avem un pătrat înscris

în triunghi cerc distanța de la

centrul pătratului la o latură

a sa este apotema pătratului în

acest caz om putem să ducem 4 apotemei

toate acestea vor fi congruente

și nu uiti ma figure avem un hexagon

hexagonul este un poligon cu șase

laturi înseamnă că într un hexagon

putem să ducem șase apotemei toate

vor fi congruente și în acest caz

punctul m este situat la mijlocul

laturii hexagonului deoarece triunghiul

c o d este un triunghi isoscel

segmentele desenat punctat sunt

raze și le sunt congruente în continuare

discutăm despre poligoane regulate

în cazul general în care avem n

laturi pentru a obține un poligon

regulat cu n laturi procedăm în

felul următor împărțim un cerc

în n arce congruente unim punctele

de diviziune și obținem astfel

laturile Poligonului care vor fi

coardele cercului laturile Poligonului

sunt congruente pentru că subîntinde

arce de aceeași măsură unghiurile

Poligonului vor fi și acestea congruentei

pentru că ele cuprinde între laturile

lor ace de măsuri egale în continuare

ne propunem să determinăm o formulă

Generală de calcul pentru Măsura

unui unghi al unui poligon și pentru

măsura unghiului la centru având

în vedere că sunt en ar Ce înseamnă

că măsura unui arc a1 a2 va fi

egală cu 360 de grade supra end

pentru că un cerc întreg are 360

de grade atunci măsura unghiului

la centru a unui ou A2 ma fie egală

cu 360 de grade supra n pentru

că unghiul la centru are măsura

egală cu măsura arcului cuprins

între laturile sale Așadar măsura

unghiului a1 a2 va fi egală cu

360 de grade supra n să calculăm

în continuare Măsura unui unghi

al Poligonului de exemplu unghiul

a1 a2 a3 Acesta este un poligon

cu n vârfuri și n laturi de ce

avem n arce de măsuri egale Măsura

unui unghi situat pe cerc este

jumătate din măsura arcului cuprins

între laturile sale dar arcul cuprins

între laturile acestui unghi este

arcul mare a 1-a na3 având în vedere

că aici avem deja două arce a1

a2 respectiv a2 a3 înseamnă că

arcul mare a 1 a n a 3 conține

n minus 2 arse și atunci măsura

acestui arc mare a1a na3 va fi

egală cu n minus 2 ori măsura unui

arc adică 360 de grade supra n

Măsura unui unghi înscris în cerc

este jumătate din măsura arcului

cuprins între laturile sale astfel

măsura unghiului a1 a2 a3 ma fie

egală cu 1 pe 2 ori măsura arcului

mare a 1-a na3 și egal cu 1 supra

2 pe lângă n minus 2 ori 360 de

grade supra n se simplifică 2 cu

360 și obținem n minus 2 ori 180

de grade supra n aceasta va fi

formula de calcul pentru Măsura

unui unghi al unui poligon cu n

laturi dacă doiul să calculăm suma

măsurilor unghiurilor unui astfel

de poligon o să înmulțim Măsura

unui unghi cu n pentru că în total

avem n unghiuri în total sunt n

unghiuri atunci suma măsurilor

acestor ape care o sănătescu sa

fie egală cu n ori A minus 2 ori

180 de grade supra n se simplifică

n cu N și obținem n minus 2 ori

180 de grade în concluzie putem

să anunțăm aceste proprietăți Măsura

unui unghi al unui poligon regulat

cu n laturi este n minus 2 ori

180 de grade supra n suma măsurilor

unghiurilor unui poligon cu n laturi

este n minus 2 ori 180 de grade

și unghiul la centru corespunzător

fiecărei laturi are măsura de 360

de grade supra n astfel dacă ne

propunem să calculăm de exemplu

Măsura unui unghi al unui octagon

octogonul fiind un poligon cu opt

laturi înlocuim în această formulă

pe n cu numărul 8 și obține Măsura

unui unghi al octogonului în continuare

o să calculăm latura apotema și

aria unui poligon cu n laturi înscris

în cerc în funcție de raza cercului

circumscris Poligonului presupunem

că avem aici un poligon cu n vârfuri

și n laturi am notat primele patru

vârfuri cu a b c și d am dus apotema

om perpendiculară pe AB segmentele

punctate o a o b o c și o d sunt

raze Pentru început o să deducem

o formulă de calcul pentru latura

acestui poligon în funcție de raza

cercului circumscris mai întâi

remarcăm faptul că triunghiul AOB

este un triunghi isoscel pentru

că are două laturi congruente o

a și o b o m este înălțime în acest

triunghi isoscel prin urmare om

va fi mediană și bisectoare să

scriem aceste lucruri triunghiul

AOB este isoscel iar om este perpendiculară

pe ab prin urmare om este și mediană

adică a m va fi egal cu MB cu alte

cuvinte punctul m este mijlocul

laturii AB și om va fi și bisectoare

a unghiului aob asta înseamnă că

om în parte Unghiul aob în două

unghiuri congruente a o m și m

o b Așadar măsura unghiului a o

m a fi egală cu măsura unghiului

b o m scene ala cu jumătate din

măsura unghiului AOB am văzut mai

devreme că măsura unghiului la

centru este 360 de grade supra

n decedat mai departe cu jumătate

1 pe 2 ori măsura unghiului aob

și egal cu 1 pe 2 ori 360 de grade

supra n se simplifică 2 cu 360

și obținem 180 de grade supra n

aceasta este măsura unghiului b

o m în triunghiul dreptunghic b

o m o să aplicăm o funcție trigonometrică

pentru a determina lungimea laturii

m d pentru că ne interesează o

relație între latura Poligonului

și rază o să aplicăm funcția trigonometrică

sinus aceasta se definește ca raportul

dintre cateta opusă unghiului ascuțit

și ipotenuza În triunghiul dreptunghic

m o b sinusul unghiului b o m este

cateta opusă unghiului b o m adică

m b supra ipotenuza OB rezultata

sinus de 180 de grade supra n este

egal cu MB supra raza cercului

OB este rază din această relație

exprimăm lungimea segmentului MB

aceasta este egală cu raza ori

sinus de 180 de grade supra n pe

noi ne interesează ab latura Poligonului

aceasta a se obține dublul lungimea

laturii m b pentru că m este mijlocul

lui AB prin urmare latura Poligonului

adică a fi egală cu 2 ori r ori

sinus de 180 de grade supra n aceasta

este formula de calcul pentru Latura

unui poligon cu n laturi în funcție

de raza cercului circumscris acestuia

în continuare o să determinăm o

formulă de calcul pentru apotema

Poligonului în funcție de raza

pentru aceasta o să aplicăm o altă

funcție trigonometrică și anume

funcția trigonometrică cosinus

În triunghiul dreptunghic m o b

cosinusul unghiului b o m este

raportul dintre cateta alăturată

supra ipotenuză cateta alăturată

este om iar ipotenuza este o b

obținem astfel cosinus de 180 de

grade supra n egal cu om Care este

apotema Poligonului supra o b care

este rază din această relație exprimăm

apotema aceasta este egală cu aer

ori cosinus de 180 de grade supra

and am obținut și formula de calcul

pentru apotema Poligonului în funcție

de raza cercului circumscris în

continuare o să determină și formula

de calcul pentru aria acestei poligon

dacă Poligonul are n laturi și

unim punctul O cu fiecare vârf

al Poligonului obținem n triunghiuri

triunghiul AOB este unul din aceste

triunghiuri și atunci aria Poligonului

se obține însumând ariile celor

n triunghiuri Deci aria Poligonului

va finală cu n ori aria triunghiului

AOB triunghiul AOB are baza AB

și înălțimea om și atunci Momi

exprimă aria acestui triunghi ca

fiind Sami produsul dintre apotema

Poligonului și latura Poligonului

aria Poligonului este n ori aria

triunghiului aob egal cu n ori

aria triunghiului AOB este baza

ori înălțimea supra 2 ab ori om

supra 2 egal Putem să scriem n

supra 2 ori ab este latura Poligonului

iar om este apotema Poligonului

egal cu m supra doi în loc de el

o să scrie formula pe care am determinată

2r sinus de 180 de grade supra

n ori în loc de apotemă scrie în

formula r ori cosinus de 180 de

grade supra n egal 2:02 se simplifică

și obținem e n ori aer la a doua

cosinus de 180 de grade supra n

ori cosinus de 180 de grade supra

n aceasta este formula de calcul

pentru aria unui poligon cu n laturi

în funcție de raza cercului circumscris

acestuia de capitulăm puțin aceste

formule pe care le am de terminat

n n adică Latura unui poligon cu

n laturi este 2 sinus de 180 de

grade supra n apotema Poligonului

este raza ori cosinus de 180 de

grade supra n și aria Poligonului

este n ori el la a doua ori sinus

de 180 de grade supra n ori cosinus

de 180 de grade supra n în aceste

formule R este raza cercului circumscris

Poligonului iar n este numărul

de laturi ale Poligonului